Attention Model

本文介绍深度学习中一个常见的机制 Attention Model，以及其在实际场景中应用。因为 attention 是受到人类注意力（即 attention）机制启发的一类比较宽泛的想法，而不是一个具体的模型或者公式，本文的重点会放在如何在不同问题下设计 attention，希望给今后自己设计 attention 带来一些启发。

什么是 Attention

一般在处理图像的时候，是将图片或者图片的一部分经过预处理，作为一个整体输入到模型当中，输入层图片的不同位置没有任何区分，模型（比如 CNN）在处理的时候可能会给图片的不同区域不同的权重。然而，人眼在处理的图片的时候，首先会将注意力集中在图片的某个感兴趣的区域上，并且模糊区域周围的图片，即人眼直视的区域和余光的区别。attention Model 就是受到人的注意力机制的启发，显示地模拟注意力的方法。同样，在自然语言处理（NLP）领域中，attention 机制也很多应用，事实上现在主流的 NLP 模型都会在某一步中用到 attention。比如在神经机器翻译任务（Neural Machine Translation, Attention Model” 翻译为“注意力模型”，显然 “attention” 这个词对“注意力”这个翻译相比“Model”起到了更大的（决定性的）作用。在问答系统（Question and Answering, QA）中，我们需要关注的往往是问题里的关键词，像是 a, and, the 这一类的 stop words 往往不是非常重要。

总结来说，attention Model 就是在传到模型下一层之前，给予 input features 不同的权重（attention）的方法。这个方法灵活性很大，input features 可以是模型最开始输入层的数据，也可以是中间某一个隐藏层的一系列特征向量。同时，计算权重的方法也多种多样。下面会具体介绍一些论文中设计 attention Model 的方法。

Recurrent Models of Visual Attention

这篇论文是 attention 在图像处理领域的应用。这里有一个 Pytorch 写的代码，训练30个 epochs 内能达到还不错的结果。

人在观察一幅图像时，会首先关注图像的一个区域，然后转向下一个感兴趣的区域，并重复这个过程直到掌握足够多的信息。受到这个现象的启发，本文将图像处理的过程转换为：(1) 从上一部选择的图片的区域中提取信息；（2）根据信息选择下一个区域，以及一个可能的环境动作。这个 sequential 过程用 RNN 来表示，并在 Reinforcement Learning （RL）的框架下训练，被称作 Recurrent Attention Model （RAM）。这里图片的区域相当于 RL 中的 Observation，State 是之前所有的历史信息，选择下一个区域和环境动作是 Actions。由于这篇博客的重点是 attention，就不详细介绍 RL 了。环境动作根据不同的任务有不同的设置。如果是一个分类问题，本文中会首先固定这个过程一共执行多少步，模型只会在最后一步时选择环境动作，这个动作是图片分类的结果。如果 RAM 模型应用在电子游戏中，环境动作就是可操纵物体的动作，比如上下左右之类的，而这个动作可能会影响到图片（即 Environment）本身，这也就是说在 RAM 中提供区域的图像本身也会随着整个过程变化。RL 的奖励（Reward）根据任务不同也有不同的设置，比如在图片分类中，本文设置最后分类正确的奖励是1，分类错误，以及之前所有步骤的奖励都是0。RAM 可以有效地减少计算量，因为每次输入的可以是一个固定大小的区域，这样计算就和图片大小本身没有关系。

上述过程可以总结为如下几步，在第 t 步时：

计算 feature。根据当前图片 $x_t$ 和上一步中得到的位置动作 $l_{t-1}$, 可以得到一个局部的 retina-like representation $\rho(x_t, l_{t-1})$。这里$\rho$是一个越远离中心 $l_{t-1}$ 像素越低的图像表示，在论文里被称作 glimpse，起到模拟 attention 机制的作用，同时达到了减少输入维度的效果。结合局部图像表示与位置信息，通过 glimpse network $f_g$ 得到 glimpse feature $g_t = f_g(x_t, l_{t-1}; \theta_g)$。这里位置信息 $l_{t-1}$ 除了用于生成 $\rho_t$，还用来和 $\rho_t$ 一起生成 $g_t$，所以实际上可以表达为 $g_t = f_g(\rho(x_t, l_{t-1}), l_{t-1}; \theta_g)$。
计算当前 internal state。根据历史信息 $h_{t-1}$，通过 core network 计算出当前 state $h_t = f_h(h_{t-1}, g_t; \theta_h)$。
计算下一个位置 $l_t$ 和动作 $a_t$。位置 $l_t$ 从一个由 location network 定义的概率分布中抽样 $l_t \sim p(\cdot | f_l(h_t; \theta_l))$。动作 $a_t$ 从一个由 action network 定义的概率分布中抽样 $a_t \sim p(\cdot | f_a(h_t; \theta_a))$。

训练的目标是为了得到一个概率策略（stochastic policy）$\pi((l_t, a_t) | s_{1:t}; \theta)$ 来最大化期望奖励 $\mathbb{E}_{p(s_{1:T}; \theta)}[R]$，这里 $s_{1:t}$ 代指之前的所有动作，位置，图片信息 $(l_i, a_i, x_i)$，$p(s_{1:T}; \theta) = \Pi_{t=1}^T \pi((l_t, a_t) | s_{1:t}; \theta)$。参考 Variational Autoencoder 中公式(4)的推导，可以得到目标函数的 gradient
$$\nabla_{\theta} J = \sum_{t=1}^{T} \mathbb{E}_{p(s_{1:T}; \theta)} [\nabla_{\theta} \log \pi((l_t, a_t) | s_{1:t}; \theta)R] \simeq \frac{1}{M} \sum_{i=1}^{M} \sum_{t=1}^{T} \nabla_{\theta} \log \pi((l_t, a_t)^{i} | s_{1:t}^i; \theta)R^i \tag{1}$$

用来自论文的示意图来表示上述流程：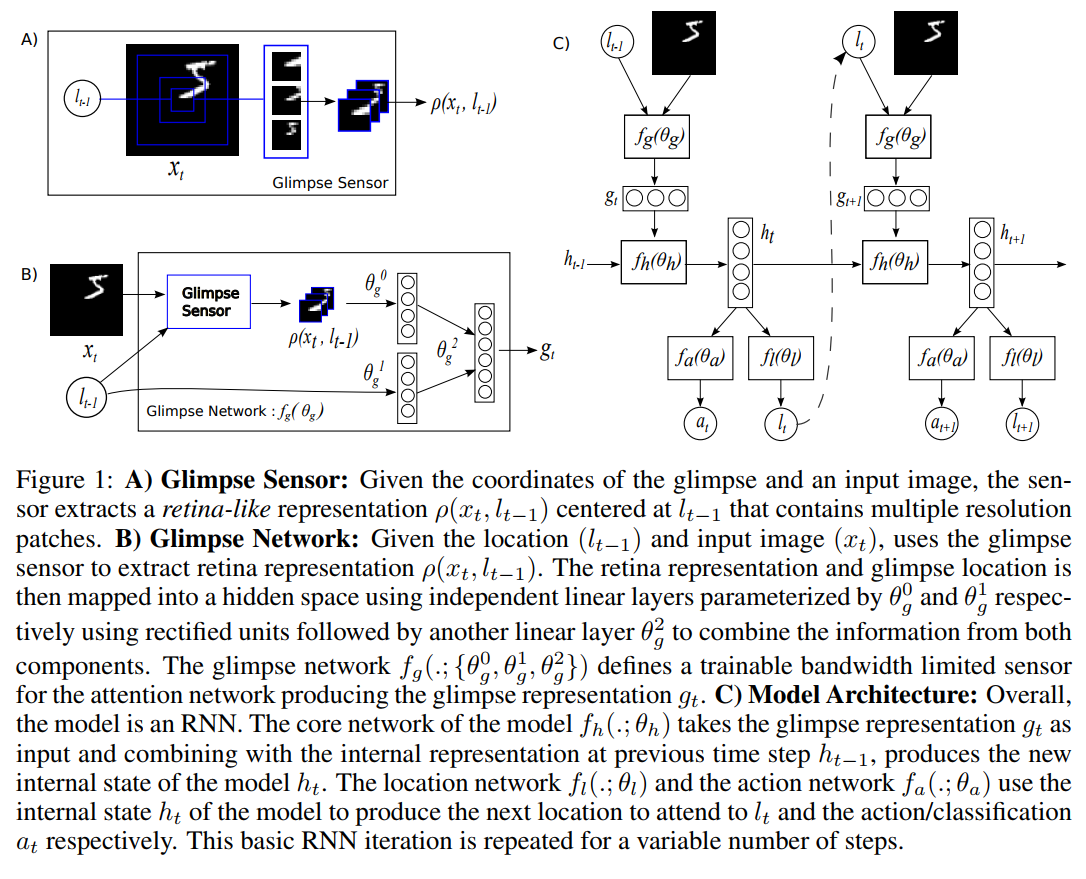
Recurrent Attention Model

具体到图像分类问题和电子游戏问题中的 $f_*$ 如何定义，原文中有详细的描述，这里就不重复了。值得注意的是，在图像分类问题中，Local network $f_l$ 可以用公式(1)来训练，$f_a$ 则通过由 cross entropy loss 定义的分类损失函数训练。

RAM 中， attention 加在模型的输入层，attention 的权重与当前输入图片和前一步计算得到的图片位置有关，通过一个 reccurrent 的结构计算加权后的输入 $\rho(x_t, l_{t-1})$。

Neural Machine Translation By Jointly Learning To Align And Translate

这篇文章是 attention 在 NMT 中的应用，应该是最早的一篇 attention 在深度 NLP 中的应用。

这篇文章发表之前效果做好的 NMT 模型使用的是 Encoder-Decoder 结构，参见 Cho et al. 和 Sutskever et al.。简单来说，模型中的 Encoder 负责将输入文本 encode 成一个固定长度的向量 $c$，并期望其中包含了输入文本的全部信息；Decoder 负责将 $c$ decode 成目标语言语句。由于语言本身的 sequential 特性，Encoder 和 Decoder 可以用 RNN 结构实现，比如 LSTM、 biLSTM，当然现在 CNN 也有很大的优势。下面以 RNN 为例给出一个比较正式的 Encoder-Decoder 定义。

Encoder-Decoder 结构

给定一个句子 $\mathbf{x} = (x_1, x_2, …, x_T)$ ，这里 $x_t$ 是一个单词的词向量（embedding）。Encoder 以这个句子作为输入，利用 RNN 将其 encode 为一个向量 $c$，具体有
$$h_t = f(x_t, h_{t-1})$$

$$c = q(h_1, h_2, …, h_T)$$

其中 $h_t$ 是 RNN 的 hidden state。上面提到的两个论文都是用 $q(h_1, h_2, …, h_T) = h_T$ 的形式。接下来，利用另一个 RNN 来生成/预测目标语言的结果 $\mathbf{y} = (y_1, y_2, …, y_T)$。RNN 定义了一个条件概率函数
$$p(\mathbf{y}) = \Pi_{t=1}^T p(y_t | y_1, y_2, …, y_{t-1}, c)$$

$$p(y_t | y_1, y_2, …, y_{t-1}, c) = g(y_{t-1}, s_t, c) \tag{2}$$

$$s_t = f’(s_{t-1}, y_{t-1}, c) \tag{3}$$

其中 $s_t$ 是 RNN 的 hidden state，$g$ 是一个 softmax 分类器。

Attention

Encoder-Decoder 结构有一个问题，就是无论句子有多长，最后得到的都是一个固定长度的向量，那么长句子所得到的向量中每个词的信息就会少。同时，在第一节翻译的例子也提到，输入句子中不同的词，对于输出翻译句子中的不同的词的贡献是不一样的，这一点在 Encoder-Decoder 中没有得到体现，因为无论生成的哪一个 $y_t$，输入句子提供的信息都是 $c$。attention Model 可以帮助解决这个问题。不过 attention 在本文中是被称作 alignment，即翻译中的每个词和输入的每个词对齐，意思上感觉差不多。

本文中将 Decoder 中的条件概率（公式(2)）和 RNN （公式(3)）改为
$$p(y_i | y_1, y_2, …, y_{i-1}, \mathbf{x}) = g(y_{i-1}, s_i, c_i) \tag{4}$$

$$s_i = f’(s_{i-1}, y_{i-1}, c_i) \tag{5}$$

这里 Encoder 不在生成唯一的向量 $c$，而是针对不同的 $s_t$，利用所有的 hidden state $\lbrace h_1, h_2, …, h_T \rbrace$ 生成
$$c_i = \sum_{j=1}^{T_{x}} \alpha_{ij}h_j \tag{6}$$

$\alpha_{ij}$ 就是本文中 attention 的权重，由如下公式计算得到
$$\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{T_{x}} \exp(e_{ik})}$$

$$e_{ij} = a(s_{i-1}, h_j)$$

其中函数 $a(\cdot)$ 可以是一个神经网络。这里作者期望 $a(\cdot)$ 可以学习到对于接下来要生成的词 $y_i$，哪一个输入单词（的 hidden state）更重要。论文中的 Figure 3 证明该模型确实学习到了单词的对应关系。

用来自论文的示意图来表示 attention 部分，因为论文中使用的是 biLSTM，所以隐藏层有两层，不过原理是一样的，$h_t = [\overrightarrow{h_t};\overleftarrow{h_t}]$ 由两个方向的 hidden state 首尾相接而成。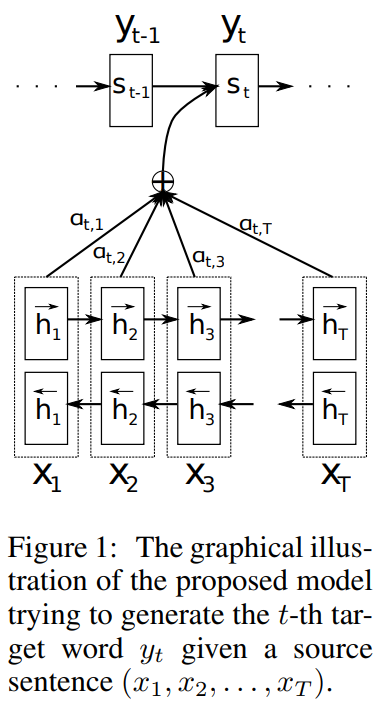
Encoder-Decoder attention

该模型中， attention 加在模型的 Encoder 和 Decoder 中间，attention 权重与 RNN 模型前一个输入和当前 hidden state 有关，通过一个神经网络计算 $a(s_{i-1}, h_j)$。

Bi-Directional Attention Flow For Machine Comprehension

这篇文章是 attention 在 Question Answering (QA) 中的应用，用到一个著名的 QA 数据集，Stanford Question Answering Dataset (SQuAD)。SQuAD 数据集由 Wikipedia 的文章 context，与文章相关的问题 query 以及答案组成，其中问题的答案是该文章中的一段话。解决 QA 问题的模型需要根据问题和文章内容，输出答案在文章中的开始位置和结束位置。这篇文章中用到的 attention 我觉得还是很合理的，比较有借鉴意义。

模型结构

本文的模型一共分为6层，这里先简单介绍一下模型的结构，之后重点解释一下和 attention 相关的运算。模型有两个输入，context sentence $\lbrace \mathbf{x_1}, \mathbf{x_2}, …, \mathbf{x_T} \rbrace$ 和 query sentence $\lbrace \mathbf{q_1}, \mathbf{q_2}, …, \mathbf{q_J} \rbrace$。之后各自经过三种（算作3层） embedding layers, character embeddings with CNN, pretained word embedding 和 contextual embedding using bi-LSTM 得到两组 embedding vectors：context vectors $\mathbf{H} \in \mathbb{R}^{2d \times T}$ 和 query vectors $\mathbf{U} \in \mathbb{R}^{2d \times J}$。接下来，经过 Attention Flow Layer，得到 query-aware context vectors $\mathbf{G} \in \mathbb{R}^{* \times T}$，也就是说利用 query vectors，通过一种加权的方法，得到了新的 context vectors。之后 $\mathbf{G}$ 会传入由 bi-LSTM 组成的 Model Layer，得到加入 attention 后的 context vectors 的 contextual embedding $\mathbf{M} \in \mathbb{R}^{2d \times T}$，和之前的第3层起到同样的效果。最后由 $\mathbf{G}$ 和 $\mathbf{M}$ 一起通过一个 softmax function 得到起始位置，M 经过另一个 LSTM 得到进一步的 encoding vectors $\mathbf{M}^2$，由 $\mathbf{G}$ 和 $\mathbf{M}^2$ 得到终止位置。论文中的模型示意图如下

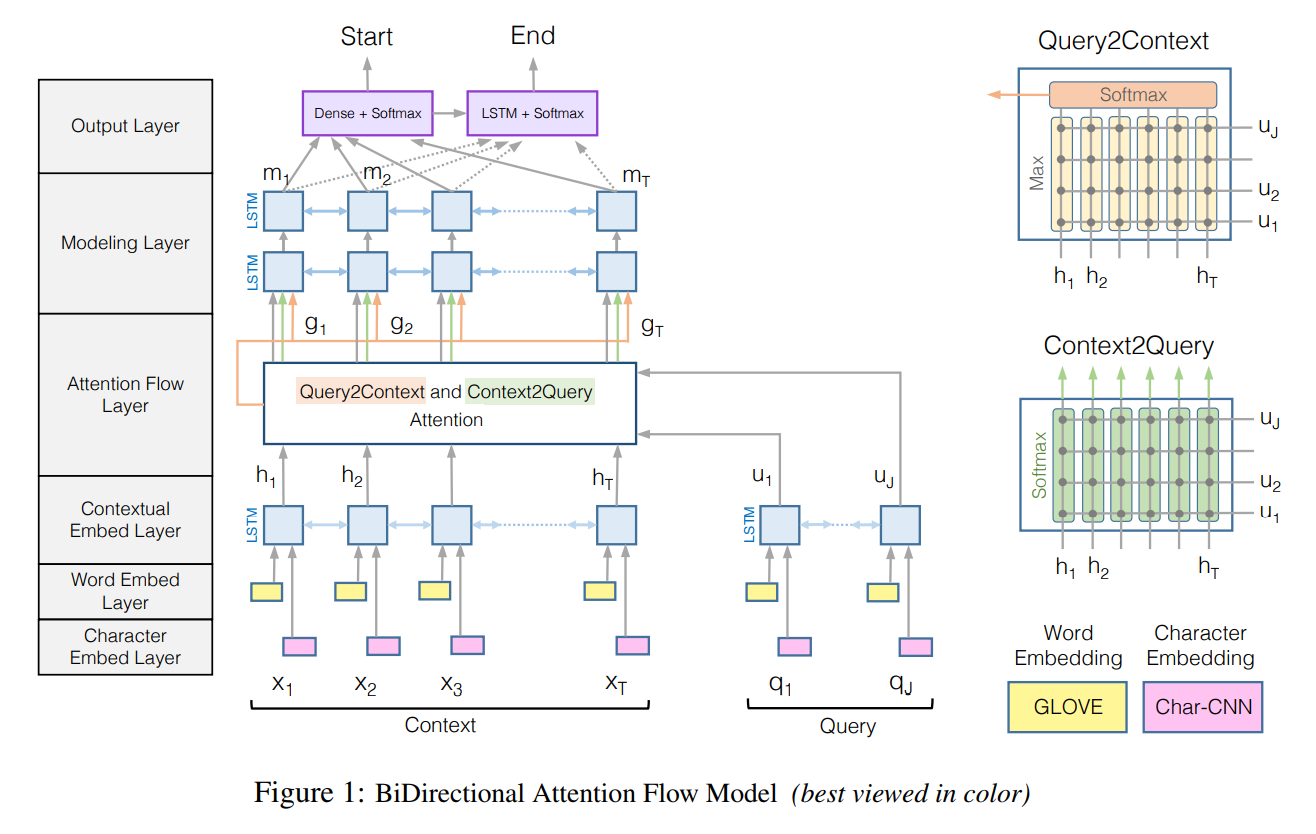
Bi-Directional Attention Flow For Machine Comprehension

Bi-Attention

Bi-Attention 指的两个方向的 attention，Context-to-query Attention 和 Query-to-context Attention，简单的总结一下就是 query vectors 关于每个 context word 的加权求和（一共 T 个），以及根据 query 得到 context words 中单词重要程度的加权求和（1个）。

为了计算 Bi-Attention，首先需要得到一个 context words 和 query words 的相似度矩阵（similarity matrix） $\mathbf{S} \in \mathbb{R}^{T \times J}$，其中 $\mathbf{S}_{tj}$ 是 context 中第 t 个单词和 query 中第 j 个单词的相似度。论文中相似度由一个线性函数 $\alpha$ 计算得到：
$$\mathbf{S}_{tj} = \alpha(\mathbf{H}_{:t}, \mathbf{U}_{:j}) = \alpha(\mathbf{h}, \mathbf{u}) = \mathbf{w}_{(\mathbf{S})}^T [\mathbf{h};\mathbf{u};\mathbf{h} \circ \mathbf{u}]$$

其中 $[\mathbf{h};\mathbf{u};\mathbf{h} \circ \mathbf{u}]$ 是向量 $\mathbf{h}$，$\mathbf{u}$，$\mathbf{h} \circ \mathbf{u}$ 首尾相连得到，$\circ$ 代表 element-wise 乘法。论文中的 Figure 3 证明这样得到的相似度矩阵确实起到了预想中的作用。

Context-to-query Attention (C2Q)。 对于一个 context word，C2Q 能够计算出我们更需要关注/注意哪一个 query word。$\mathbf{a}_t \in \mathbb{R}^J$ 表示给定第 t 个 context word 时 query words 的注意力权重（attention weights），$\mathbf{a}_t = \text{softmax}(S_{t:})$。这个公式的意思是，注意力权重 $\mathbf{a}_t$ 的大小由第 t 个 context word 和每个 query words 的相似度大小决定。之后，我们就能计算出与第 t 个 context word 相关的 query words 的加权平均（文中称为 attended query vectors） $\tilde{\mathbf{U}}_{:t} = \sum_j a_{tj} \mathbf{U}_{:j}$。$\tilde{\mathbf{U}} \in \mathbb{R}^{2d \times T}$。

Query-to-context Attention (Q2C)。 Q2C 只得到一个向量，这个向量表达的是所有跟 query 相关的 context words 的加权平均，即从文章中选出对问题很重要的那些单词。Attention weights $\mathbf{b} = \text{softmax}(\max_{\text{col}} (\mathbf{S})) \in \mathbb{R}^T$，其中 $\max_{\text{col}} (\mathbf{S})$ 的第 t 个维度 $\max_{\text{col}} (\mathbf{S})_t$ 表示的是第 t 个 context word 与所有 query words 的相似度 $\mathbf{S}_{t:}$ 中最大的那个，也就是第 t 个 context word 与问题中最相关的单词的相关度。$\mathbf{b}_t$ 可以作为第 t 个 context word 与问题相关性的一个度量。这样，我们可以计算出 $\tilde{\mathbf{h}} = \sum_t \mathbf{b}_t \mathbf{H}_{:t} \in \mathbb{R}^{2d}$，表示所有context 中与问题相关的单词的集合。$\tilde{\mathbf{H}} \in \mathbb{R}^{2d \times T}$ 是 $\tilde{\mathbf{h}}$ 重复 T 遍的结果。

最后，我们可以用$\mathbf{H}_{:t}$，$\tilde{\mathbf{U}}_{:t}$ 和 $\tilde{\mathbf{H}}_{:t}$ 来表示加入 attention 信息后的第 t 个 context word vector $\mathbf{G}_t = \beta(\mathbf{H}_{:t}, \tilde{\mathbf{U}}_{:t}, \tilde{\mathbf{H}}_{:t}) \in \mathbb{R}^{*}$，这其中蕴含了第 t 个单词的 embedding 本身，所有与该词相关的 query words 的信息，以及整个文章 context 中与问题 query 有关的单词的信息。本文用的是$\beta(\mathbf{H}_{:t}, \tilde{\mathbf{U}}_{:t}, \tilde{\mathbf{H}}_{:t}) = [\mathbf{h};\tilde{\mathbf{u}};\mathbf{h} \circ \tilde{\mathbf{u}};\mathbf{h} \circ \tilde{\mathbf{h}}] \in \mathbb{R}^{8d}$。从直觉上来说，我感觉文章单词的 embedding 和 $\tilde{\mathbf{H}}_{:t}$ 应该没有多大关系，因为它表示的是整篇文章（关于问题）的信息。结果（Table 1b）也证明了 C2Q 确实更重要一点，不过 Q2C 也会提高模型的效果就是了。

该模型中的 attention 是双向的。我们会根据问题，重点关注文章中的某些单词（Q2C）；在浏览文章中的每一个单词时，我们则会考虑它和问题中的哪一部分相关（C2Q）。

Attention Is All You Need

标题口气不小，实际来看标题大概想表达的是 attention is all they used。这篇文章仍然是 attention 在 NMT 上的应用，不同于之前的模型，他们提出的模型 Transformer 没有用到 convoluion 或者 recurrent layer，而是利用 attention 来完成所有的工作，并取得很好的效果。在文章第四章中，作者讨论了为什么用 attention 来替代 CNN 或 RNN，其中一个最大的原因就是获得 long-range dependencies 所需要的计算量。如果句子长度为n，那么 RNN 需要 $O(n)$ 次 recurrent 计算才能获得首尾单词的 dependency，dilated CNN 需要 $O(\log_kn)$ 次 convolution 计算当 kernel 大小是 $k$ 时。而本文中提出的 self-attention 只需要常数次运算。另外还有一点就是 RNN 的计算方式不利于大规模并行实现。

本文首先对 attention 做了一个定义。一个 attention function 将一个 query，几对儿 key-values 映射到一个 output。其中 query, keys, values, output 都是向量。output 是 values 的一个加权求和，其中权重是由 query 及对应的 keys 计算的来的。文章并没有给出这么定义的 intuition，实验部分也没有特别给出关于 query, keys, values 的可视化表示，只能说非常遗憾。有了 Attention 的定义之后，输入维数为 $d_k$ 的 query， $s \times d_k$ 的 keys 向量，以及 $s \times d_v$ 的 values 向量（这里 $s$ 是 key-value pairs 的数量，论文中并没有明确地表示出来），文章定义 Scaled Dot-Product Attention
$$\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$$

其中 $\sqrt{d_k}$ 是为了防止 gradient saturation 的一个 trick。

文章利用 Scaled Dot-Product Attention 定义了 Multi-Head Attention 作为模型中的 attention function，作者只提出这么做效果会好，并没有说明为什么，以及是怎么想到的。在我看来这个 Multi-Head 实际上和 CNN 里面多个 kernel 的效果是一样的，不同 Head 捕捉不同的信息。正式定义如下，假设使用 $h$ 个 Head：
$$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, …, \text{head}_h) W^O$$

$$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$$

模型仍然是一个 Encoder-Decoder 结构，不同的是，Decoder 利用上三角 mask 矩阵得到一个 auto-regressive 的结构，从而达到预测输出的第 i 个词的时候 $\text{Attention}[i::] = 0$，这是为了保证预测不依靠句子后面单词的信息。除此之外还有一系列的 trick，感觉也是谷歌典型的那种天花乱坠的结构 + 复杂 engineering 的模型。这里有一个 pytorch 的实现，对了解模型中用到的 trick 和理解整个模型很有帮助。总体结构如下图所示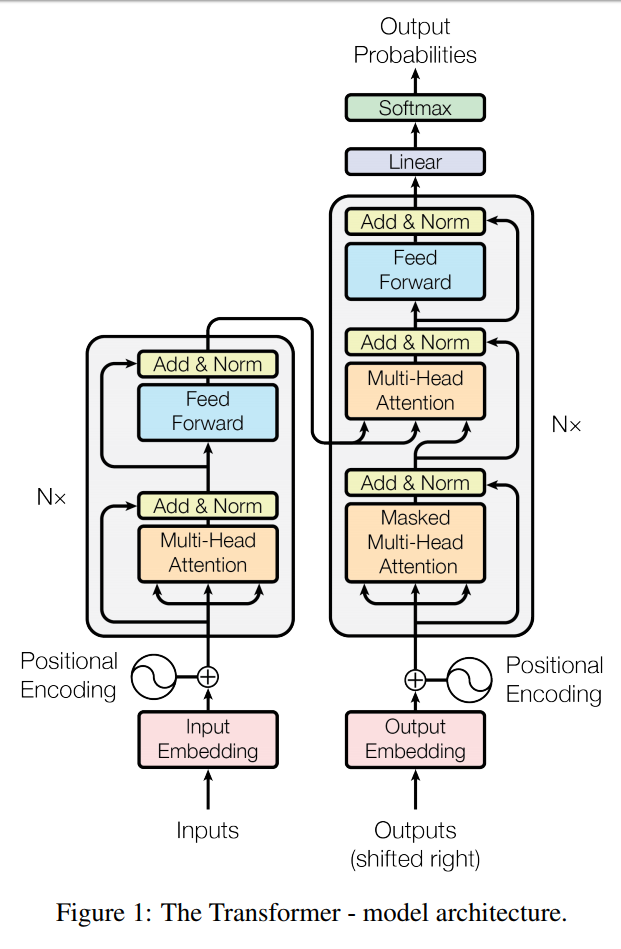
Attention Is All You Need

从图中可以看出，Encoder 中 Multi-Head Attention 输入的 Q, K, V 均为输入的 input，文章中称为 self-attention。Decoder 中同样含有 self-attention，同时还有使用 Encoder 的输出作为 V 和 K 的另一种 Attention 模式。

总结

Attention 的形式多种多样，本文介绍了4种在不同领域中应用 Attention 取得更好效果的模型。简单来说， Attention 是根据不同的上下文环境（context）改变模型某一层输入的方法，这种改变可以是加权平均，也可以是更加复杂的方法，比如 Google 的 Multi-Head Attention，或者像是第一篇中剪裁不同位置的图片。在自然语言处理中，上下文环境一般是指语境，在 QA 问题中，问题和原文可以互为环境。Attention 的目的是根据不同的环境区分输入，从而更好的利用输入信息。