在现实任务中,智能体间的合作是至关重要的。比如,在足球游戏中,球员们除了发挥个人能力外,也需要通过传球配合的方式进攻。本文的主题是,如何利用强化学习构建具有合作能力的多智能体(multi-agent)系统。在这样的系统设置下,每个单智能体(single-agent)只能接触到部分状态信息(POMDP问题),单纯的最大化单智能体的期望回报可能与系统整体利益不符,因此直接使用一般的单智能体强化学习算法很难起效。下面将介绍3种模型,他们采取不同的方法构建智能体间的通信机制,实现了期望的合作行为。
Value-Decomposition Networks For Cooperative Multi-Agent Learning (论文)
如果想要使用基于价值的强化学习模型(value-based),就需要对系统的联合动作-价值函数(joint action-value function,联合$Q$函数)建模。假设系统中有$d$个智能体,则联合$Q$函数可以表示为$Q((h_1, h_2, …, h_d), (a_1, a_2, …, a_d))$,其中$h_i$表示智能体的局部信息,$a_i$表示动作。可以看出,如果使用一般的方法建模,$Q$函数的输出维度是$d^n$,$n$是动作空间的维度。
Value-Decomposition Networks(VDN)的基本假设是,系统的联合$Q$函数可以近似为多个单智能体的$Q$函数的和:
$$Q((h_1, h_2, …, h_d), (a_1, a_2, …, a_d)) = \sum_{i=1}^d {Q}_i (h_i, a_i)$$,
其中${Q}_i$之间是独立的,只取决于局部观策和动作$h_i, a_i$。这样可以保证,最大化每个单智能体的${Q}_i$函数得到动作,与通过最大化联合$Q$函数得到的结果是一样的,即
$${\max}_{\boldsymbol{a}} Q = {\max}_\boldsymbol{a} \sum_{i=1}^d Q_i = \sum_{i=1}^d {\max}_{a_i} Q_i$$
$${\text{argmax}}_{\boldsymbol{a}} Q = ({\text{argmax}}_{a_i} Q_i)$$
我们可以通过全局的奖励函数,间接地训练每个单智能体的$Q$函数。并且只要对每个智能体选择最大化${Q}_i$的动作,就能使得全局$Q$值最大。
文章中还提到,结合以下的技巧,VDN能够得到更好的效果:
- 使用DRQN作为$Q$函数。经试验证明,使用 LSTM 作为$Q$函数网络的输出层在 PODMP 环境下有更强的鲁棒性和泛化能力。
- 参数共享(weight sharing)和角色信息(role information)。即所有的单智能体使用同一个$Q$函数网络,同时在输入中加入一个 one-hot 向量来区别不同角色的智能体。
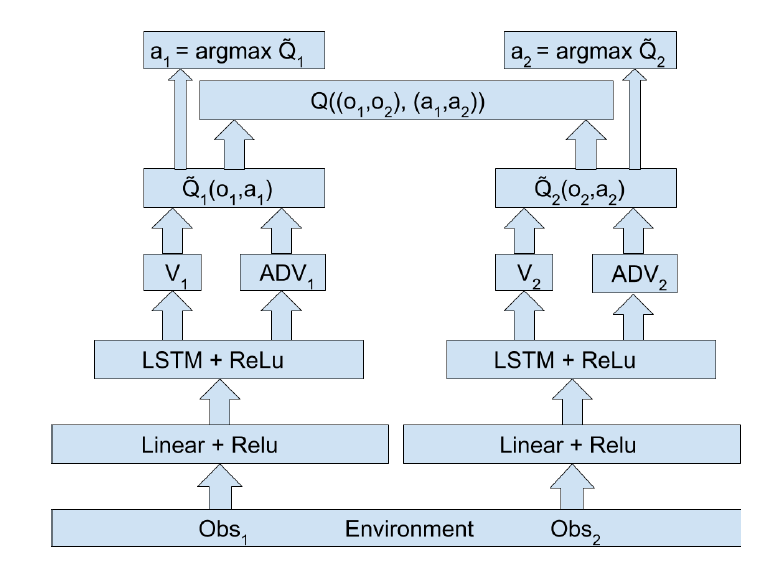
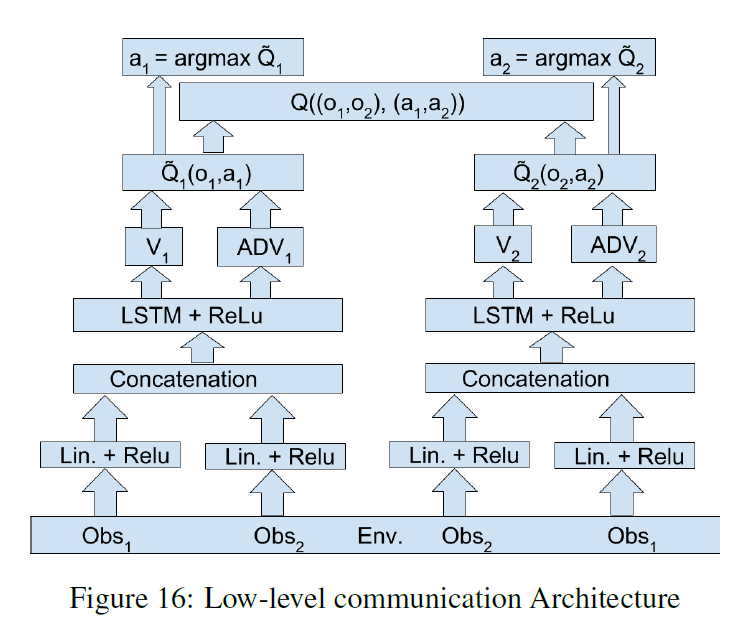
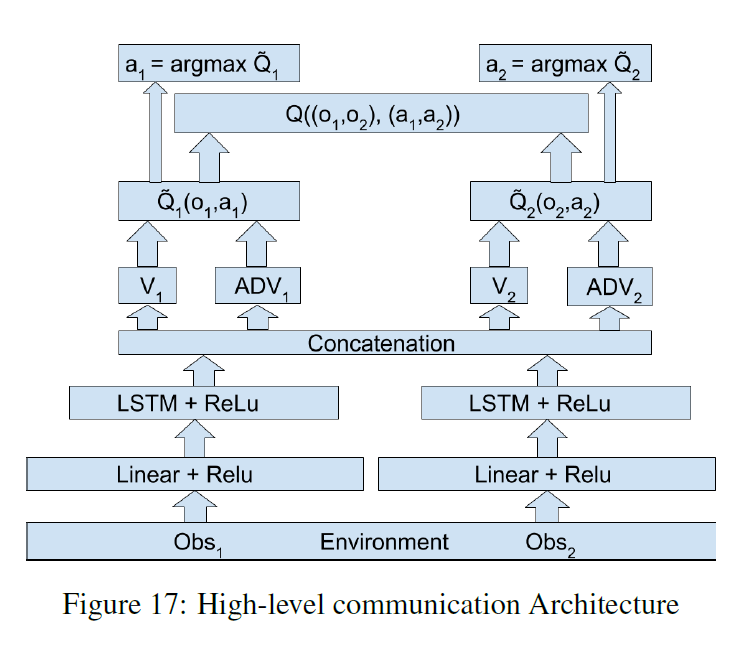
- 智能体间的通信(information channels)。本文试验了两种通信方式,一种是在输入时就包括了其他智能体的信息(low level),另一种是结合$Q$网络的高层隐藏变量(high level)再分别输出。
下面的3张图分别是 VDN, VDN + low level communication, VDN + high level communication 的网络结构。
QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning (论文)
VDN 可行的原因可以总结为一个公式:
$${\text{argmax}}_{\boldsymbol{a}} Q = ({\text{argmax}}_{a_i} Q_i)$$
即联合$Q$函数取最大值等价于每个$Q_i$函数取最大值。
VDN 中联合函数的表达形式(求和)满足这个条件,但求和这种方式表现力有限,并不能涵盖更加复杂的组合情况,比如非线性组合。事实上,只要满足Q对于任意一个$Q_i$是单调增的(monotonic),$Q_i$和$Q$满足
$$\frac{\partial Q}{\partial Q_i} \ge 0 \text{ , } \forall a \in A$$
上述等价关系就是成立的。可以看出,VDN 中的求和形式是该条件的一个特例($\frac{\partial Q}{\partial Q_i} = 1$)。QMIX 模型的核心思想就是在$Q$和$Q_i$之间构造一个单调映射。
具体的,QMIX 模型由2部分组成,agent networks 输出单智能体的$Q_i$函数,mix network 以$Q_i$作为输入,用于计算联合$Q$函数。为了满足单调的限制,mix network 每一层的参数均由一个 hypernetwork 计算生成。hypernetworks 以当前状态$s$作为输入,输出一个与 mix network 当前层形状相匹配的向量作为参数。 hypernetworks 隐藏层的激活函数是非负的(比如 ReLU),这样得到的 mix network 每一层的参数也都是非负的,从而保证了单调的条件(bias 没有限制)。QMIX 模型结构如下图所示
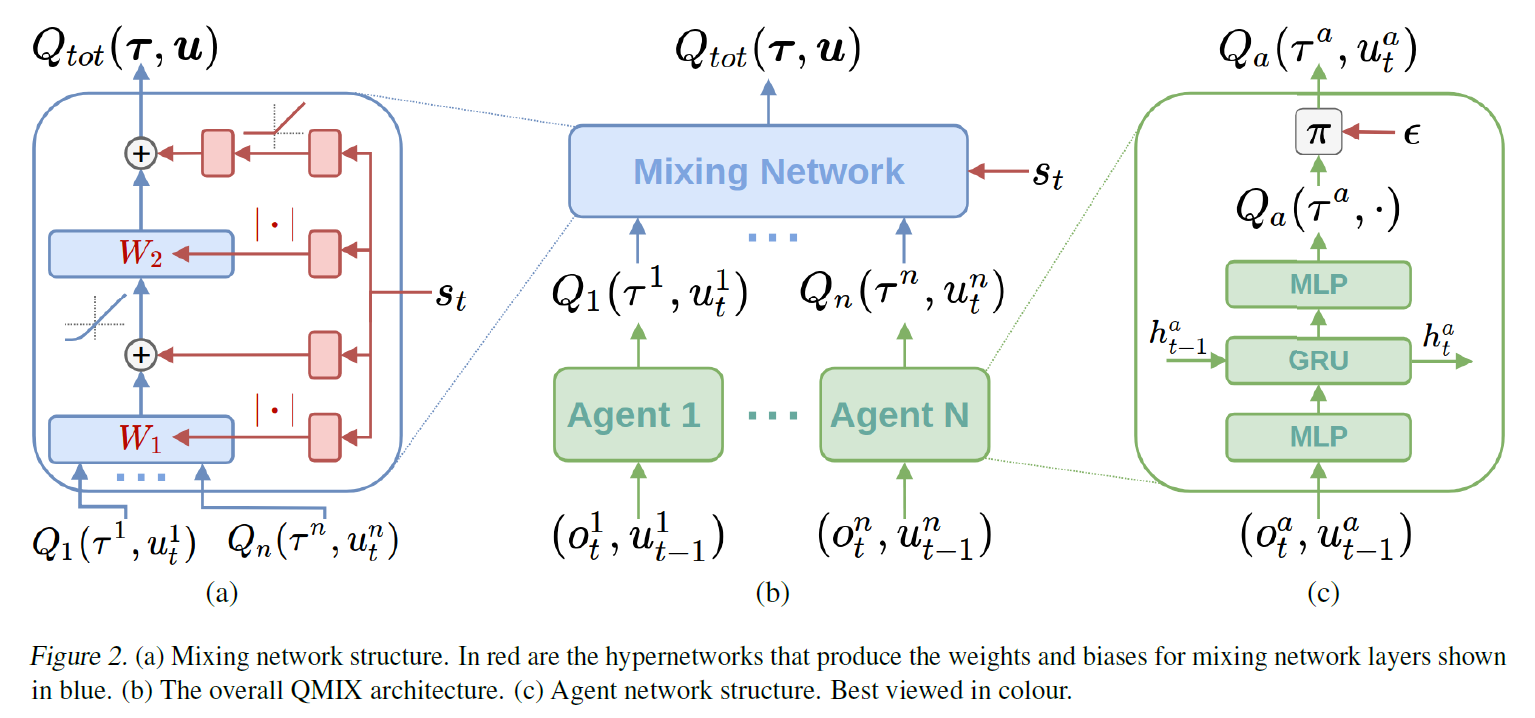
与 VDN 相比,QMIX 改进了联合$Q$函数的形式,融合了部分全局信息,使得模型的性能有很大的提升。这里需要注意的是,agent networks 并没有使用全局信息,所以这还是一个 POMDP 环境。
Counterfactual Multi-Agent Policy Gradients (论文)
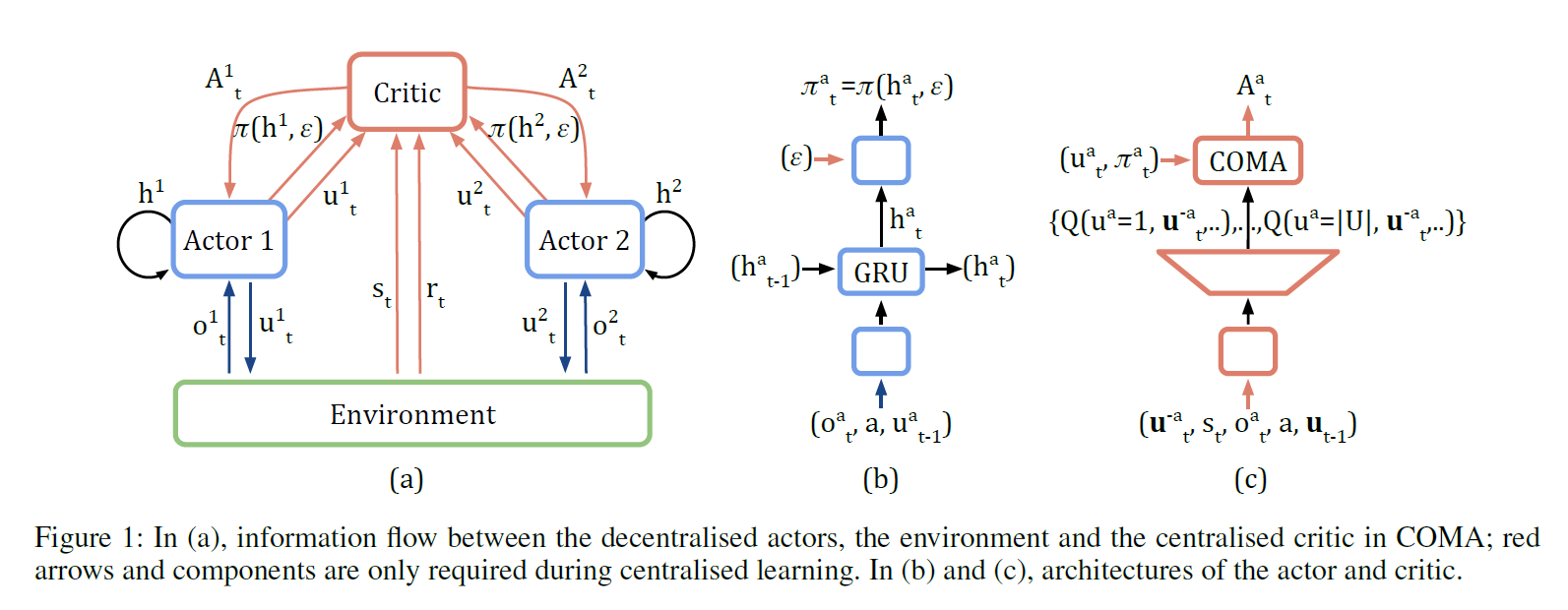
VDN 和 QMIX 都采用了这样一种结构:中心化计算系统的$Q$函数,单智能体的$Q_i$函数去中心化或者说因子化(factored)。这种结构使得策略在训练的时候可以利用全局信息,同时每个智能体仍然只接受局部信息作为输入。类似的,在 Actor-Critic 框架中,我们同样可以通过分散 Actor, 中心化 Critic 来达到同样的效果,COMA 就采用了这样的思想。此外,COMA 还考虑了另外一个问题:如何合理的分配全局系统奖励(credit assignment)。每个智能体对全局奖励的贡献是不同的,在更新 Actor 网络时,应该考虑到这种不同,分配合理的奖励给不同的 Actor。
COMA 的做法是,对于一个智能体,计算一个动作的优势函数(advantage function),文章里称为 counterfactual baseline。函数计算,固定其他智能体的动作时,一个智能体的某个动作的Q值与所有动作Q值平均值间的差
$$A^a (s, \boldsymbol{u}) = Q (s, \boldsymbol{u}) - \sum_{u’^{a}} \pi^a(u’^{a} | \tau^a) Q (s, (\boldsymbol{u}^{-a}, u’^{a})$$
这里$a$表示某个智能体,$\boldsymbol{u}$表示所有智能体的动作,$\boldsymbol{u}^{-a}$表示除了$a$之外的所有智能体的动作。
我觉得使用优势函数的动机是,如果智能体做任何动作得到的全局奖励都差不多,那么它的 Actor 这次就不需要太多的更新。为了简化计算,Critic 不会计算所有智能体动作组合的Q值(输出维度是$|U|^n$个),而是针对每一个智能体,将其他智能体的动作当作输入,输出该智能体每个动作对应的$Q$值(输出维度降为$|U|$)。COMA 的结构如下图所示
实现
幸运的是,有人做过 VDN,QMIX 和 COMA 之间在星际II上的效果对比,还开源了模型和环境。VDN 和 QMIX 的实现比较直观,每个智能体都是一个独立的 DRQN 模型,有一个 mixer 融合所有的Q值。COMA 的实现要更有技巧一些,里面用到好多 masking 的方式来区分 Critic 网络的输入属于哪一个智能体。从效果上看,QMIX 要好于 VDN 和 COMA,毕竟它是最后发表的,在 QMIX 文章中也提到 on-policy 模型可能带来 sample-inefficiency 问题。